Prefix Linear Attention Can Outspeed Causal Linear Attention

Notes on Prefix Language Modeling--and a surprising observation that PrefixLM can be *faster* than Causal LM under some architectural conditions.

This blog post describes 1) my opinions on Prefix Language Modeling objectives for Transformer-based decoder-only language models, and then 2) describes why this is not the case for Linear Attention-style recurrent LM architectures–PrefixLM can actually be faster than Causal LM for these architectures in some settings! Part 2) is inspired by the recent JRT-RNN paper which applies PrefixLM to Linear Attention-based recurrent models, but states a fact about extra added efficiency I could not see written out anywhere in that paper.

I’ve not gotten around to actually trying to write a more efficient impl. of prefixLM linear attention using this fact, and the class of architectures for which this should help is limited. I just wanted to write down these two observations somewhere less ephemeral.

Prerequisites: If you are unfamiliar with Linear Attention, it may help to read about the basic ideas of what it is and how it’s computed in my previous post or the papers linked in that post. I try to cover all necessary background very briefly in this post, however.

Introduction

Most current language models are trained using a Causal Language Modeling (“Causal LM”) objective. This means that they predict 1 token at a time, left-to-right.

There are other variants that have been used or proposed, ranging from the original Masked Language Modeling (MLM) or the more general T5-style Span Corruption, hybrids of causal language modeling and span corruption (Fill-In-The-Middle, GLM), mixtures of these objectives (UL2, UL2R), and more.

The one we’ll focus on in this post is Prefix Language Modeling (“PrefixLM”). See the diagram below for an image demonstrating the difference between PrefixLM and Causal LM: in PrefixLM, some initial subset of tokens may attend bidirectionally to each other (the “prefix”), followed by all other tokens being produced autogressively as in Causal LM. For more details on the other objectives, my favorite treatment of these is an in-depth study by Wang et al. (2022)I can't recommend this paper highly enough, please read it! that attempts to disentangle the role of these objectives and the architectures often associated with them, based on zero-shot performance. Others have also written well about language modeling objectives.

Diagram showing the differences in attention pattern between Causal Language Modeling ("Causal Decoder", Left) and Prefix Language Modeling ("Noncausal Decoder", Right). In Prefix Language Modeling, a set amount of tokens at the beginning of the input (here, the string "I am") are allowed to attend bidirectionally to each other, called the "prefix".

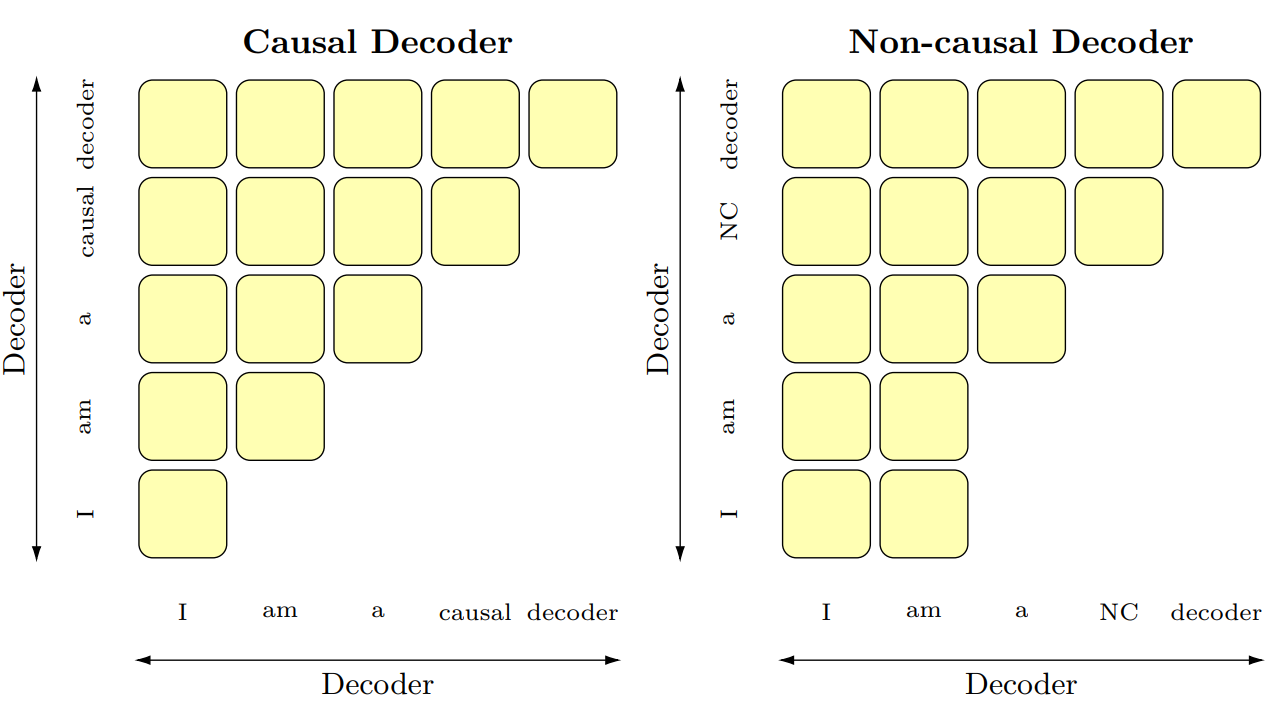
I have personally not been a fan of PrefixLM for a while, mostly because we experimented with it a bit for BLOOMZ instruction tuning (See Appendix J) and wanted it to work, but it did not clearly make a difference in downstream performance, and certainly not enough to make it worth the added overhead and potential headache. However, I don’t think this means something like PrefixLM will never be worth it in the future!

A very nice recent paper by Arora et al. (2024), JRT-RNN, actually presents a compelling case for PrefixLM being worth reevaluating for non-Transformer architectures. The authors justify their choice by showing that since optimized Linear Attention implementations are much faster than Flash Attention, they can get away with using the (typically more expensive) PrefixLM and still retain a significant speed advantage over a standard Transformer.

But there’s actually a reason that PrefixLM with Linear Attention can counterintuitively be even faster than full Causal LM, even though for softmax attention it’d be more computation! The synergy goes even deeper. I suspect the JRT-RNN authors are already aware of this fact, but I wanted to write it out so others can understand this intuition.

First, let’s briefly recap some of the disadvantages of PrefixLM for typical decoder-only GPT-style autoregressive LMs. If you are already familiar with PrefixLM and other LM objectives as well as their tradeoffs, feel free to skip to later sections.

Why Not PrefixLM For Vanilla Transformers?

Increased Costs

Flash Attention, by computing tiles of the \(L \times L\) attention matrix at a time, makes it possible to skip tiles that are fully masked out. This means we don’t have to compute anything where all positions in the tile are above the diagonal in the causal mask \(M\), and can get 2x faster attention when we’re doing fully-causal attention as compared to bidirectional attention.

For PrefixLM, although we can take advantage of some of the masked-out tiles to speed up over the fully-bidirectional case, we still are forced to compute more values that wouldn’t be needed when performing fully causal attention. And so attention with PrefixLM will be unfortunately more costly.

Also, when we’re training our model, typically we don’t get to compute any loss signal on the bidirectional-attention prefix tokens. This can reduce the number of tokens we learn from, which (might!) make training using PrefixLM less data-efficient than Causal LM.

Extra Test-Time Hyperparameter Tuning

PrefixLM also introduces a hyperparameter that must be fiddled with ($l \in [1, L]$ determining that $x_{\lt l}$ is treated as the bidirectional-attention “prefix”), either to get the best output quality, or to not push the model out-of-distribution from the typically fixed $l$ value used during training. This is not a problem Causal LM faces!

Headaches with KV Caching

If, when running our model for some use case like a multi-turn conversation, we wish to go back and change our value of $l$, then we must re-encode the entire input to create a new KV cache, rather than simply appending to the KV cache. This is an additional slowdown and cost that, again, Causal LM sidesteps.

Unconvincing Empirical Improvements

These issues would be ignorable if PrefixLM gave us much better models than Causal LM did.

However, the empirical results in do not suggest this is the case:

Zero-shot average results obtained by Wang et al. (2022). Among Causal Decoder (decoder-only model trained with Causal LM), Non-causal Decoder (decoder-only model trained with PrefixLM), and Encoder-Decoder (encoder-decoder model trained with PrefixLM), the Causal Decoder is the best zero-shot model. For our purposes, the main takeaway is that PrefixLM is no more performant than Causal LM, and can in fact underperform it.

A key caveat: These evals in Wang et al. (2022) are only loglikelihood-based classification, and are not especially high scores across the board at the scale tested in the paper. Papers like UL2R have shown improvements from training or fine-tuning on PrefixLM or other non-causal objectives, although others anecdotally have had trouble reproducing this in their own codebases. It may be the case that either at larger scales, or on generative tasks / more subjective qualities, PrefixLM or other non-causal objectives lead to noticeable improvements–we as a community don’t currently know for sure.

PrefixLM <3 Linear Attention

Recap: What is Linear Attention?

Standard Softmax attention is given by the followingWe elide the scaling of $QK^T$ by $\frac{1}{\sqrt{d}}$ for simplicity.:

\[O = \text{Softmax}\left(QK^T\right)V\]

where $Q, K, V \in \mathbb{R}^{L \times d}$.

Linear attention makes this more efficient by replacing the Softmax function with a feature map \(\phi: \mathbb{R}^d \to \mathbb{R}^{d'}\) applied to Q and K separately:

\[O = \frac{(\phi(Q)\phi(K)^T) V}{\phi(Q)\sum^L_{i=1}\phi(K_i)^T}\]

where \(Q, K \in \mathbb{R}^{L \times d'}, V \in \mathbb{R}^{L \times d}\).

This allows us to re-associate \((\phi(Q)\phi(K)^T) V\) as \(\phi(Q)(\phi(K)^T V)\), letting us avoid the \(O(L^2)\) complexity of softmax attention by never producing the intermediate \((\phi(Q)\phi(K)^T) \in \mathbb{R}^{L \times L}\).

In practice it has been found that one can get away with avoiding the denominator terms:

\[O = \phi(Q)(\phi(K)^T V)\]

so we’ll simplify Linear Attention to this going forward.

Causality and Chunked Algorithm

When we perform causal language modeling, we introduce a mask $M$ that prevents tokens from being affected by future tokens in the sequence:

\[O = \text{Softmax}\left(QK^T \odot M \right)V\]

However, when we introduce this causal mask $M$ into linear attention:

\[O = (\phi(Q)\phi(K)^T \odot M) V\]

We can no longer reorder the matmuls \((QK^T)V\) as \(Q(K^T V)\) freely! This forces us to not use the efficient form (\(O(Ldd')\)), and instead use a chunked form interpolating between purely-recurrent and purely-parallel forms:

For each chunk$[c]$ indicates the $c$-th "chunk", a.k.a. the span of indices from $[(c-1)C + 1, cC]$. $c$ can range from $1$ to $L//C$., we compute the starting state for that chunk, reusing the state computed for the chunk prior:

\[S_{[c+1]} = S_{[c]} + \sum_{i=((c-1)C + 1)}^{cC}\phi(k_i)^Tv_i = S_{[c]} + \phi(K_{[c]})^T V_{[c]}\]

and then to compute this chunk’s output $O_{[c]}$:

\[O_{[c+1]} = \phi(Q)_{[c+1]}S_{[c]} + (\phi(Q)_{[c+1]}\phi(K_{[c+1]})^T \odot M)V_{[c+1]}\]

we use the quadratic form (now quadratic in chunk size, not the entirety of $L$) while applying our causal mask $M$.

This algorithm has \(O((L//C)(C^2d' + Cdd')) = O(LCd' + Ldd')\) complexity, times $L//C$ chunks. $C$ is a tunable parameter between $1$ and $L$ determining the chunk size $L // C$.

Avoiding Chunking With PrefixLM

But for PrefixLM, the non-causal input component has no attention mask!This may note always be the case, sadly, if we want to pack multiple documents together without allowing them to attend across documents.... but it will for some cases, like, say, prefilling a super-long input for a PrefixLM Linear Attention model.. So we can freely compute in our more efficient ordering for that entire prefix component of the computation.

This means that, on the entirely non-causal input (say, up to positions $\lt j$ ) we can use the naive \(O(Ldd')\) complexity algorithm to compute the final state all in one go! No need to tamp down quadratic complexity by chunking.

We can simply compute our state $S_{\lt j}$ via

\[S_{\lt j} = \phi(K_{\lt j})^TV_{\lt j}\]

Because we attend bidirectionally to all tokens $x_{\lt j}$, the state $S_{\lt j}$ is the singular state used for computing all outputs from the prefix!)

Then, the output from our bidirectional linear attention is just:

\[O_{\lt j} = \phi(Q_{\lt j})(\phi(K_{\lt j})^TV_{\lt j}) = \phi(Q_{ \lt j})S_{\lt j}\]

Which is \(O(Ldd')\) complexity and consists of simply 2 matrix multipllies! So on the bidirectional components of PrefixLM, it can be faster to compute bidirectional Prefix Linear Attention than its causal form! This is in contrast to softmax attention, where PrefixLM requires strictly more computation than Causal LM.

Caveats

One major caveat of the speedup I’ve just explained is that many of the more recent and most performant linear attention variants use data-dependent state updates. This could hinder the usefulness of the previous observation. For example, in GLA, the original Linear Attention time-invariant state update rule:

\[S_t = S_{t-1} + k_{t}^Tv_{t}\]

becomes the time-dependent update rule

\[S_t = G_{t} \odot S_{t-1} + k_{t}^Tv_t\]

–based on some parameter calculated as a function of the current input, we decide how much to retain or “forget” the existing state when updating it with our new input. This is sometimes called different things like (data-dependent) “gating”, “decay”, or “selection” by various architectures.

It’s not especially clear that one would want a data-dependent update like this when attending to inputs bidirectionally though–maybe we can get away with data-independent updates when encoding our prefix, but include this gating when attending causally to the output. Hydra may offer some hints here.

Conclusion

In short–PrefixLM can sometimes grant a speedup over Causal LM for recurrent architectures, by removing the need to perform the chunked algorithm and directly computing the full input’s ending state! This flips the situation as compared to softmax attention, where PrefixLM is slower than Causal LM. So while it might be hard to justify for Transformers, it’s potentially easier to for Linear Attention!

Acknowledgements

Thank you to Dan Goldstein for reading an early version of this blog post!